Примеры решений задач по высшей математике
На этой странице мы собрали простые и сложные примеры из курса высшей математики - от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.
Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.
Далее решенные задачи по темам:
Высшая математика. Комплексные числа
Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 - z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.
$$ z_1 = 2 e^{-\pi i}, z_2=4 e^{\pi i}.$$Все решения о комплексных числах
Высшая математика. Матрицы
Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.
$$A= \begin{pmatrix} 1 & 2 & 1 & -1\\ 1 & 1 & 0 & 0\\ 0 & 2 & 0 & -1\\ 1 & 1 & 1 & 0\\ \end{pmatrix} $$Высшая математика. Определители
Задача. Вычислить определитель матрицы $A$
$$A= \begin{pmatrix} 4 & 5 & 6 & 5 & 11\\ 1 & 4 & 2 & 0 & 13\\ 1 & 1 & 0 & -1 & 5\\ 3 & 2 & 3 & 0 & 7\\ 4 & 1 & 2 & 3 & 8\\ \end{pmatrix} $$Высшая математика. Системы уравнений
Задача. Исследовать на совместность и решить систему уравнений:
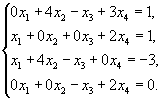
Все решения по линейной алгебре
Высшая математика. Векторы
Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.
$$X=(-4;4;4), a=(3;1;0), b=(-1;0;6), c=(-1;2;0).$$Все решения по векторной алгебре
Аналитическая геометрия на плоскости
Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $\cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Все решения по АГ на плоскости
Аналитическая геометрия в пространстве
Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.
Все решения по АГ в пространстве
Высшая математика. Пределы
Задача. Найти предел функции
$$ \lim_{x\to \infty}\left(\frac{3x^2+1}{3x^2-x+1} \right)^{3x+4}. $$Высшая математика. Производные
Задача. Найти производную от следующей функции
$$ y=\left[\sqrt[3]{\frac{1}{7+x^2}}+\frac{\sqrt{x}}{\sqrt{x}+1} \right]\cdot 24; \quad y'(1). $$Высшая математика. Исследование функции
Задача. Провести полное исследование функции и построить график.
$$y=\frac{x}{\sqrt{x^2+x}}.$$Все решения на исследование функции
Высшая математика. Интегралы
Задача. Найти неопределенный интеграл $$\int\frac{4x^2+7x-23}{(x^2-4x+8)(x+1)^2}dx.$$
Высшая математика. Применение интегралов
Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:
$$ x=3(1-\cos t)\cos t, \quad y=3(1-\cos t)\sin t, \quad 0\leq t \leq \pi. $$Все решения о применении интегралов
Высшая математика. Ряды
Задача. Исследовать сходимость числового ряда
$$\sum_{n=1}^{\infty} u_n=\sum_{n=1}^{\infty}\frac{2n+1}{\sqrt{n 2^n}}.$$Высшая математика. Дифференциальные уравнения
Задача. Найти общее решение линейного дифференциального уравнения первого порядка
$$ xy'+x^2+xy-y=0.$$Все решения по дифф.уравнениям
Высшая математика. Теория вероятностей
Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.
Все решения по теории вероятностей

