Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.

В этой статье мы рассмотрим задачи вида
"задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)".
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Далее:
- Базовые события, обозначения и формулы
- Последовательно или параллельно?
- Усложняем схему цепи
- Примеры решений
- На закуску: схема с мостиком
- Полезные ссылки
- Решебник
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем - формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$\overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $\overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,...,n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(\overline{A_i})=q_i=1-p_i$, $i=1,2,...,n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи - именно такие):
$$ P(A \cdot B) = P(A) \cdot P(B); \quad(1) $$ $$ P(A+B) = P(A)+P(B)-P(A)\cdot P(B); \quad(2) $$ $$ P(A_1+A_2+...+A_n)=1-P(\overline{A_1})\cdot P(\overline{A_2})\cdot ... \cdot P(\overline{A_n}). \quad(3) $$Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение

Элементы цепи "нанизаны" на провод один за другим (следуют один за другим, отсюда и "последовательно"). Если откажет один любой - ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 \cdot A_2 \cdot A_3$, а вероятность работы цепи равна
$$ P(X)=P(A_1 \cdot A_2 \cdot A_3)= P(A_1) \cdot P(A_2) \cdot P(A_3) =p_1 \cdot p_2 \cdot p_3. $$Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$ P(X) = p_1 \cdot p_2 \cdot ...\cdot p_n; \qquad P(\overline{X})=1-p_1 \cdot p_2 \cdot ...\cdot p_n. \quad(4) $$Параллельное соединение
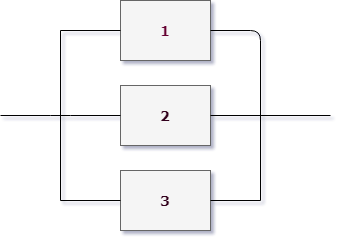
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей - это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$ P(A_1+A_2+A_3)=1-P(\overline{A_1})\cdot P(\overline{A_2}) \cdot P(\overline{A_3})=1-q_1 \cdot q_2 \cdot q_3. $$И обобщим на случай $n$ параллельных элементов в цепи:
$$ P(X) = 1-q_1 \cdot q_2 \cdot ...\cdot q_n; \qquad P(\overline{X})=q_1 \cdot q_2 \cdot ...\cdot q_n. \quad(5) $$Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению - сумма событий.
Усложняем схему цепи
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с "тремя лампочками подряд" вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
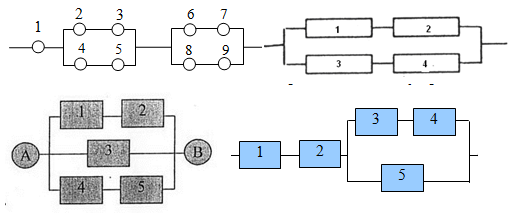
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
Возьмем для примера левую верхнюю схему:
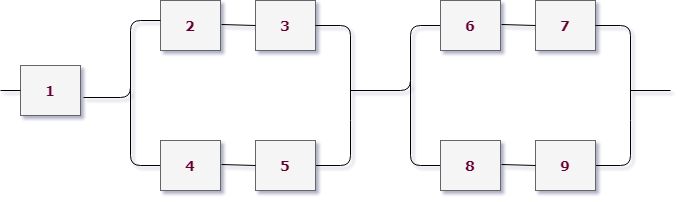
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
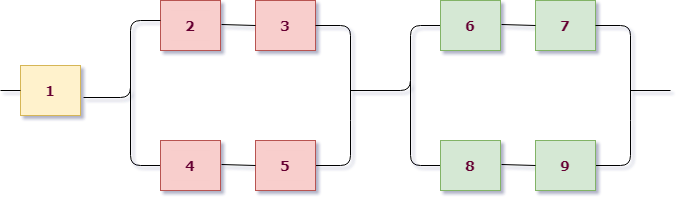
То есть тип схемы на первом уровне - последовательный:

Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$ X=X_1 \cdot X_2 \cdot X_3, $$
$X_1$ - работает первая группа элементов,
$X_2$ - работает вторая группа элементов,
$X_3$ - работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
А вот дальше интереснее. Рассмотрим поближе вторую группу:
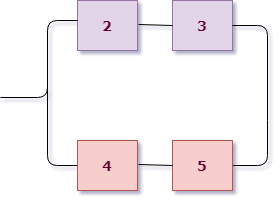
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они "висят" на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает - $A_4 \cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает - $A_2 \cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 \cdot A_3 + A_4 \cdot A_5.$$Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 \cdot A_7 + A_8 \cdot A_9.$$Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$ X=X_1 \cdot X_2 \cdot X_3 = A_1 \cdot \left( A_2 \cdot A_3 + A_4 \cdot A_5 \right) \cdot \left( A_6 \cdot A_7 + A_8 \cdot A_9\right). $$Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$ P(X)= P \left( A_1 \cdot \left( A_2 \cdot A_3 + A_4 \cdot A_5 \right) \cdot \left( A_6 \cdot A_7 + A_8 \cdot A_9\right) \right) =\\ = P (A_1) \cdot P \left ( A_2 \cdot A_3 + A_4 \cdot A_5 \right ) \cdot P \left( A_6 \cdot A_7 + A_8 \cdot A_9\right) = $$Для множителей с суммой событий внутри используем формулу (2):
$$ = P (A_1) \cdot \left[ P(A_2 \cdot A_3) + P(A_4 \cdot A_5) - P(A_2 \cdot A_3 \cdot A_4 \cdot A_5) \right] \cdot \left[ P(A_6 \cdot A_7) + P(A_8 \cdot A_9) - P(A_6 \cdot A_7 \cdot A_8 \cdot A_9)\right] = $$И снова раскрываем вероятности произведений:
$$ = P (A_1) \cdot \left[ P(A_2) \cdot P(A_3) + P(A_4) \cdot P(A_5) - P(A_2) \cdot P(A_3) \cdot P(A_4) \cdot P(A_5) \right] \cdot \left[ P(A_6) \cdot P(A_7) + P(A_8) \cdot P(A_9) - P(A_6) \cdot P(A_7) \cdot P(A_8) \cdot P(A_9)\right]. $$Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$ P(X)= p_1 \cdot \left[ p_2 \cdot p_3 + p_4 \cdot p_5 - p_2 \cdot p_3 \cdot p_4 \cdot p_5 \right] \cdot \left[ p_6 \cdot p_7 + p_8 \cdot p_9 - p_6 \cdot p_7 \cdot p_8 \cdot p_9\right]. $$Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
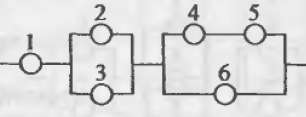
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
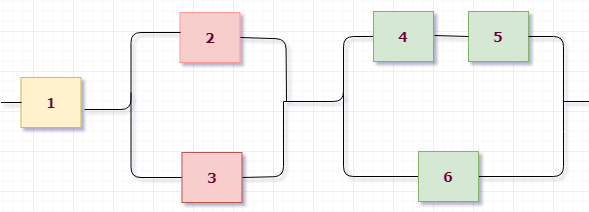
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 \cdot B_2 \cdot B_3$, где $B_i$ - работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
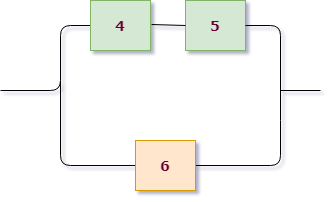
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 \cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$ B=B_1 \cdot B_2 \cdot B_3 = A_1 \cdot (A_2+A_3) \cdot (A_4 \cdot A_5 + A_6). $$Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$ P(B)=P \left( A_1 \cdot (A_2+A_3) \cdot (A_4 \cdot A_5 + A_6) \right) = P(A_1) \cdot P \left( A_2+A_3 \right) \cdot P \left( A_4 \cdot A_5 + A_6 \right) = $$Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) \cdot \left(1 - P(\overline{A_2}) \cdot P(\overline{A_3}) \right) \cdot \left( P(A_4) \cdot P(A_5) + P(A_6) - P(A_4) \cdot P(A_5) \cdot P(A_6) \right).$$Подставляем $P(A_i)=p$ и получим:
$$ p(B)=p\cdot(1-(1-p)\cdot(1-p))\cdot(p\cdot p + p -p \cdot p \cdot p) = p\cdot\left(1-(1-p)^2\right)\cdot \left(p+p^2-p^3\right). $$Осталось только найти значение при $p=0,6$:
$$ p(B)= 0,6\cdot\left(1-(1-0,6)^2\right)\cdot \left(0,6+0,6^2-0,6^3\right) \approx 0,375. $$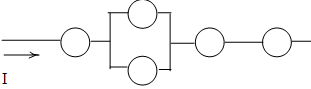
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
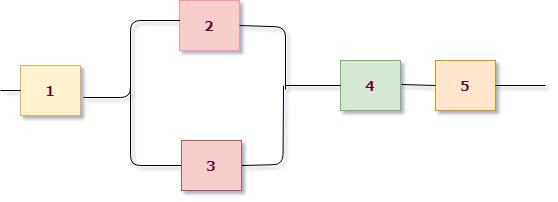
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$ X= A_1 \cdot (A_2+A_3) \cdot A_4 \cdot A_5. $$Найдем вероятность этого события (работы цепи):
$$ P(X)= P \left( A_1 \cdot (A_2+A_3) \cdot A_4 \cdot A_5 \right)= P(A_1) \cdot P(A_2+A_3) \cdot P(A_4) \cdot P(A_5)= \\ = P(A_1) \cdot \left( 1- P(\overline{A_2}) \cdot P(\overline{A_3}) \right) \cdot P(A_4) \cdot P(A_5). $$Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов - 0,8, поэтому
$$ P(X)= 0,8 \cdot \left( 1- 0,2 \cdot 0,2 \right) \cdot 0,8 \cdot 0,8 = 0,492. $$Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$ P(\overline{X}) = 1- P(X) = 1-0,492 = 0,508. $$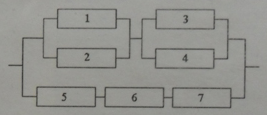
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ - работает розово-зеленая линия, $X_2$ - работает желтая.
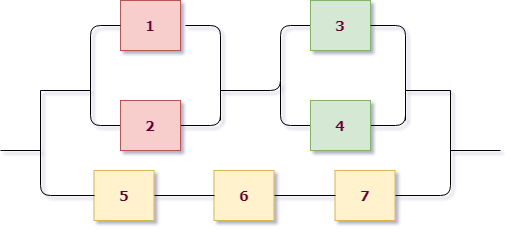
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 \cdot A_6 \cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) \cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$ X=X_1+X_2 = (A_1+A_2) \cdot (A_3+A_4) + A_5 \cdot A_6 \cdot A_7. $$Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$ P(X)= P \left( (A_1+A_2) \cdot (A_3+A_4) + A_5 \cdot A_6 \cdot A_7 \right) = \\ = P \left( (A_1+A_2) \cdot (A_3+A_4) \right) + P \left( A_5 \cdot A_6 \cdot A_7 \right) - P \left( (A_1+A_2) \cdot (A_3+A_4) \cdot A_5 \cdot A_6 \cdot A_7 \right) $$Раскрываем все произведения по формуле (1):
$$ = P (A_1+A_2) \cdot P(A_3+A_4) + P(A_5) \cdot P(A_6) \cdot P(A_7) - P (A_1+A_2) \cdot P(A_3+A_4) \cdot P(A_5) \cdot P(A_6) \cdot P(A_7) = $$По формуле (3) расписываем $P(A_1+A_2)=1-P(\overline{A_1}) \cdot P(\overline{A_2}) = 1-q_1\cdot q_2$ и $P(A_3+A_4)=1-P(\overline{A_3}) \cdot P(\overline{A_4})= 1-q_3\cdot q_4$.
Итого:
$$ P(X)= (1-q_1\cdot q_2) \cdot (1-q_3\cdot q_4) + p_5 \cdot p_6 \cdot p_7 - \\- (1-q_1\cdot q_2) \cdot (1-q_3\cdot q_4) \cdot p_5 \cdot p_6 \cdot p_7. $$Подставляем значения надежности элементов:
$$ P(X)= (1-0,2^2)^2 + 0,9^3 - (1-0,2^2)^2 \cdot 0,9^3 \approx 0,9788. $$Еще: другие уроки о решении задач по вероятности
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне - параллельную или последовательную, и весь алгоритм решения рушится.
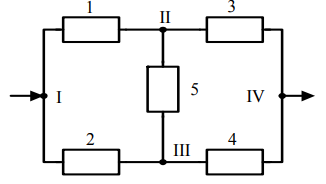
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) "портит" тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток - последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:
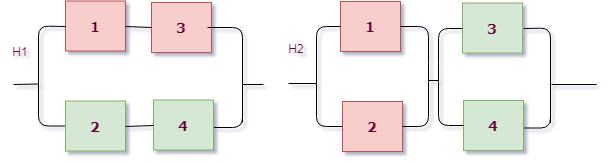
Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1\cdot A_3+ A_2\cdot A_4$, вероятность
$$ P(X|H_1) = P(A_1\cdot A_3+ A_2\cdot A_4)= P(A_1\cdot A_3)+ P(A_2\cdot A_4) - P(A_1\cdot A_3 \cdot A_2\cdot A_4)=\\ =p_1 \cdot p_3 + p_2 \cdot p_4 - p_1 \cdot p_2 \cdot p_3 \cdot p_4. $$Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$ X|H_2 = (A_1+A_2)\cdot (A_3+A_4),\\ P(X|H_2) =P( (A_1+A_2)\cdot (A_3+A_4)) = P(A_1+A_2)\cdot P(A_3+A_4)=\\ = (1-P(\overline{A_1}) \cdot P(\overline{A_2})) \cdot (1-P(\overline{A_3}) \cdot P(\overline{A_4})) = (1-q_1\cdot q_2) \cdot (1-q_3\cdot q_4). $$Тогда по формуле полной вероятности, надежность схемы равна:
$$ P(X)=P(X|H_1)\cdot P(H_1) + P(X|H_2)\cdot P(H_2) = \\ = q_5 (p_1 \cdot p_3 + p_2 \cdot p_4 - p_1 \cdot p_2 \cdot p_3 \cdot p_4) + p_5 (1-q_1\cdot q_2) \cdot (1-q_3\cdot q_4). $$Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Полезные ссылки по ТВ
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):

