Решение задачи о встрече (через геометрическую вероятность)
Полная статья о том как найти вероятность в задаче о встрече и онлайн-шаблон для чертежа.
Задача 2: Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
Решение: Используем геометрическое определение вероятности события $A$ = (Встреча с другом состоится).
Обозначим за $х$ и $у$ время прихода, $0 \leq х, у \leq 60$ (минут). В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата $ОАВС$.
Друзья встретятся, если между моментами их прихода пройдет не более 5
минут, то есть
$$y - x < 5, y >x, $$
$$x - y < 5, x > y. $$
Этим неравенствам удовлетворяют точки, лежащие в области $G$, очерченной красным.
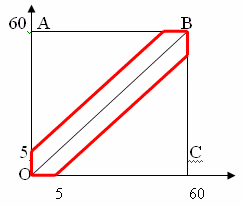
Тогда вероятность встречи равна отношению площадей области $G$ и квадрата, то есть $$P(A)=\frac{S_G}{S_{OABC}}=\frac{60\cdot 60-55\cdot 55}{60\cdot 60}=\frac{23}{144}=0,16.$$
Ответ: 0,16
Решебник по теории вероятности
Больше 16000 решенных и оформленных задач по всем темам теории вероятности в решебнике:

