Решение задач о встречах
В этой статье мы разберем возможные постановки задачи о встрече в теории вероятностей, опишем ход решения и приведем подробные примеры и дадим шаблон чертежа.
Постановка задачи
Самая популярная постановки задачи о встрече будет звучать примерно так:
Двое (студентов, влюбленных, бизнесменов) договорились встретиться под часами (на вокзале, в кафе) в интервал между X и Y часами, и каждый готов ждать другого $a$ и $b$ минут соответственно. Вопрос, с какой вероятностью они встретятся? Или разойдутся, не дождавшись другого?
Варианты из контрольных по вероятности ниже:
Какова вероятность Вашей встречи с другом, если вы договорились встретиться в определенном месте, с 12.00 до 13.00 часов и ждете друг друга в течение 5 минут?
Два лица договорились встретиться в определённом месте между 12 и 13 часами, причём каждый пришедший на свидание ждёт другого в течении 20 минут, после чего уходит. Найдите вероятность встречи этих лиц, если каждый из них приходит на свидание в случайный момент времени, не согласованный с моментом прихода другого.
Два человека прилетают в один аэропорт. Время прилета обоих равновозможно в течение часа. Какова вероятность встречи этих людей, если каждый из них ожидает выдачи багажа 20 минут (в одном и том же месте)?

Помимо этого, встречаться могут не только люди, но и пароходы:)
В любой момент времени в течение суток к причалу могут подойти независимо друг от друга два парохода. Время стоянки первого парохода 1 час, второго – 2 часа. Найти вероятность того, что одному из пароходов придется ожидать освобождения причала.
И более того, даже цифровые сигналы:), и это тоже задача о встрече.
На устройство поступают 2 сигнала, причем поступление каждого сигнала, в течение часа, равновозможно. Устройство срабатывает, если разность между моментами поступления сигналов меньше 10 минут. Найти вероятность того, что устройство сработает.
План решения задачи о встречах
А теперь перейдем непосредственно к решению этой задачи, попробуем начать с общего вида задачи и подробного алгоритма решения с помощью геометрического определения вероятности.
Задача. Двое человек договорились встретиться в интервал между 10 и 11 часами, первый готов ждать второго $a=10$ минут, а второй первого - $b=20$ минут соответственно.
1) какой вероятностью встреча случится?
2) с какой вероятностью встреча не случится?
Формализуем эту задачу. Обозначим время прихода первого человека за $x$, второго - $y$. Для удобства перейдем в минуты, тогда (так как каждый приходит с 10:00 до 11:00), можно считать, что и $x$, и $y$ случайным образом берутся в интервале от 0 до $T=60$ (минут).
Используем геометрическое определение вероятности. Рассмотрим прямоугольную систему координат $xOy$. В этой системе координат всем возможным значениям времени прихода людей $(x,y)$ соответствуют точки квадрата со стороной $T=60$.
Чертежи для наглядности будем делать на сайте Desmos.com, слева код, справа сам чертеж, ссылка на шаблон чертежа будет ниже.
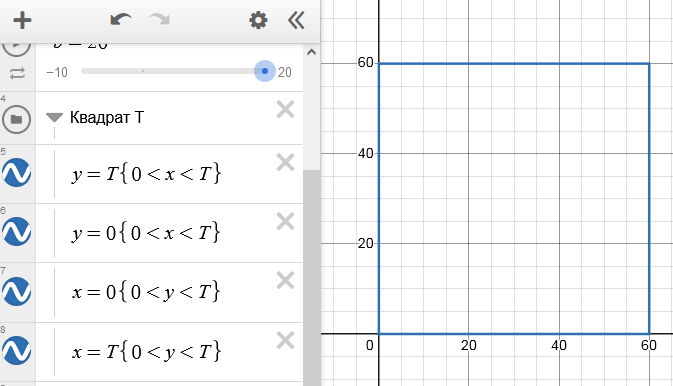
Введем событие: $A$ = (Встреча произойдет). Нужно найти множество тех точек в квадрате, которые являются благоприятствующими событию $A$
Люди встретятся, если первый пришедший дождется второго. Так как они готовы ждать разное время, возможны два случая:
если второй пришел позже первого ($y \gt x$), но не позже чем через $a=10$ минут от него: $y \lt x+10$, когда $y \gt x$
если первый пришел позже второго ($x \gt y$), не но позже чем через $b=20$ минут от него: $x \lt y+20$, когда $y \lt x$.
Более компактно запишем условия:
$$ x \lt y \lt x+a \quad \text{ или } \quad x-b \lt y \lt x. \quad (*) $$или
$$ x \lt y \lt x+10 \quad \text{ или } \quad x-20 \lt y \lt x. \quad (*) $$Построим прямые $y=x$, $y=x-20$, $y=x+10$ и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (зеленый шестиугольник в центре) являются благоприятствующими событию $A$.
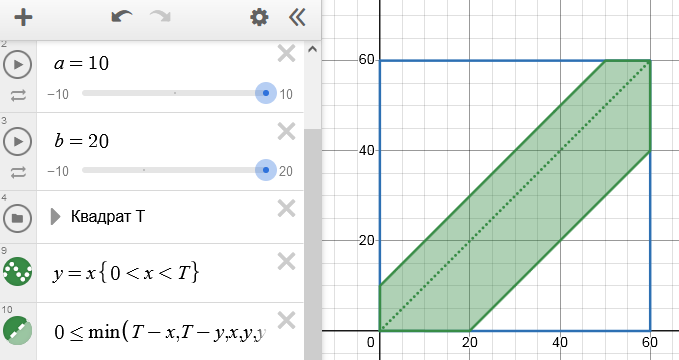
Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади всего квадрата. Проще всего найти площадь этой фигуры, вычтя из площади квадрата площади белых треугольников (сверху и снизу) со сторонами $T-a=60-10=50$ и $T-b=60-20=40$:
$$ P(A)=\frac{T^2-1/2\cdot (T-a)^2-1/2\cdot (T-b)^2}{T^2}=1-\frac{(T-a)^2}{2T^2}-\frac{(T-b)^2}{2T^2}. (**) $$или, для наших значений:
$$ P(A)=\frac{60^2-1/2\cdot 50^2-1/2\cdot 40^2}{60^2}=\frac{31}{72}=0,431. $$Осталось найти вероятность события $B$ = (Встреча не состоится) как противоположного для $A$:
$$ P(B)=1-P(A)=\frac{(T-a)^2}{2T^2}+\frac{(T-b)^2}{2T^2} $$или, для наших значений:
$$ P(B)=1-P(A)=1-0,431=0,569. $$Итоговые формулы:
$$ P(A)=1-\frac{(T-a)^2}{2T^2}-\frac{(T-b)^2}{2T^2}; \quad P(B)=1-P(A)=\frac{(T-a)^2}{2T^2}+\frac{(T-b)^2}{2T^2} (***) $$Онлайн-чертеж для задачи о встречах
По ссылке вы найдете шаблон чертежа для задачи о встречах в Desmos, где можно ввести свои параметры из задачи (интервал прихода $T$, время ожидания $a$, $b$) и получить рисунок именно для вашего случая: Задача о встрече
Примеры с пояснениями
А теперь, вооруженные теорией, формулами (***) и помощником в построении рисунков, кратко решим несколько типовых задач о встречах.
Пример 1. Два студента условились встретиться в определенном месте между 10 и 12 часами дня. Пришедший первым ждет второго в течение 1 часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает момент своего прихода (в промежутке от 10 до 12 часов)
Обозначим время прихода студентов за $x$ и $y$, так как они приходят в интервал от 10 до 12 часов - $T=120$ минут, исходная область $0 \le x \le 120$ и $0 \le y \le 120$.
Каждый ждет другого $a=b=60$ минут, поэтому строим прямые $y=x$, $y=x-60$, $y=x+60$, задающие это ограничение:
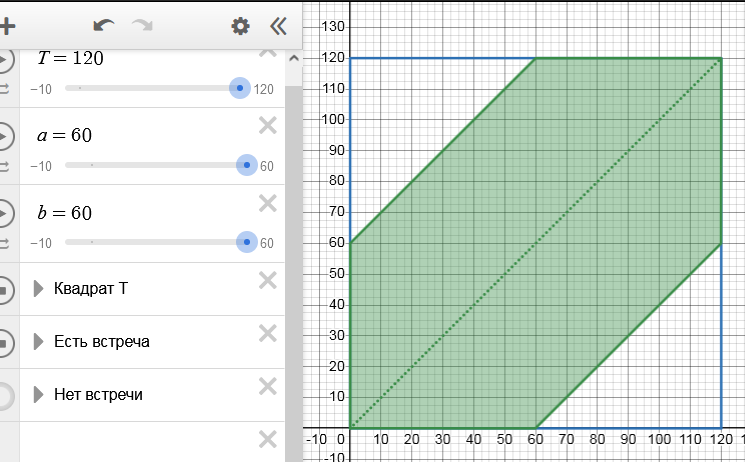
Вероятность встречи по ранее выведенной формуле равна отношению площади этой фигуры к общей площади квадрата:
$$ P=\frac{120^2-1/2\cdot 60^2-1/2\cdot 60^2}{120^2}=0,75. $$Пример 2. Два человека прилетают в один аэропорт. Время прилета обоих равновозможно в течение часа. Какова вероятность встречи этих людей, если каждый из них ожидает выдачи багажа 15 минут (в одном и том же месте)?
Обозначим время прилета за $x$ и $y$, интервал прилета - один час ($T=60$ минут), исходная область $0 \le x \le 60$ и $0 \le y \le 60$.
Каждый ждет в зоне выдачи багажа $a=b=15$ минут. Люди встретятся в зоне выдачи багажа, если
$$ x-15 \lt y \lt x+15 $$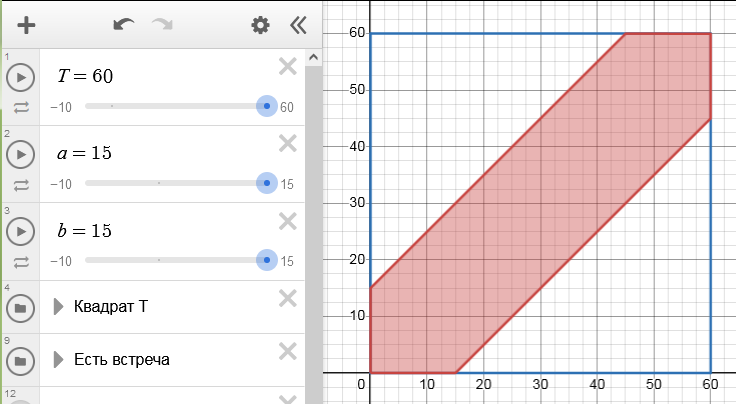
Вероятность встречи равна отношению площади закрашенной фигуры к общей площади квадрата:
$$ P=\frac{60^2-1/2\cdot 45^2-1/2\cdot 45^2}{60^2}=0,4375. $$Пример 3. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов независимо и равновозможно в течение суток. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода 3 ч, а второго 4 ч.
По факту, это та же задача о встрече, а искомая вероятность "Одному из пароходов придется ожидать освобождения причала" и есть вероятность события "Пароходы встретятся у причала".
Обозначим время прихода пароходов за $x$ и $y$. Следуя шагам формализации задачи, ввдем обозначения интервала прихода $T=24$ (часа), время стоянки пароходов $a=3$, $b=4$ (часов).
Пароходам придется ожидать друг друга, если:
$$ x \lt y \lt x+3 \quad \text{ или } \quad x-4 \lt y \lt x, \quad 0 \le x,y \le 24 $$Строим чертеж по шаблону:
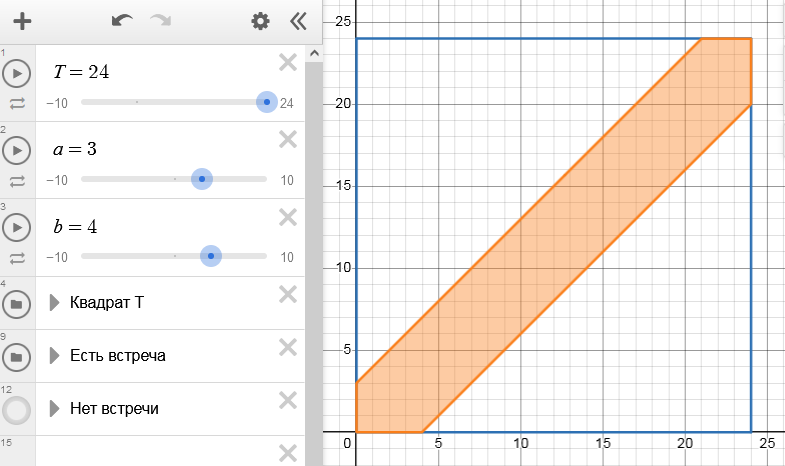
Искомая вероятность ожидания у причала по формуле (**):
$$ P=\frac{24^2-1/2\cdot 21^2-1/2\cdot 20^2}{24^2}=0,27. $$Пример 4. На устройство поступают 2 сигнала, причем поступление каждого сигнала в течение часа равновозможно. Устройство срабатывает, если разность между моментами поступления сигналов меньше 10 минут. Найти вероятность того, что устройство не сработает.
Эта задача также решается через модель геометрической вероятности и сводится к задаче о встрече. Здесь $x,y$ - время поступления сигналов, $ 0 \le x,y \le 60$ (минут). Событие $B$ = (Устройство не сработает) = (Встреча сигналов не произошла). При этом время ожидания до встречи сигналов задано и равно $a=b=10$ (минут).
Строим чертеж, закрашиваем уже область, где "нет встречи":
$$ y \lt x-10 \quad \text{ или } \quad y \gt x+10 $$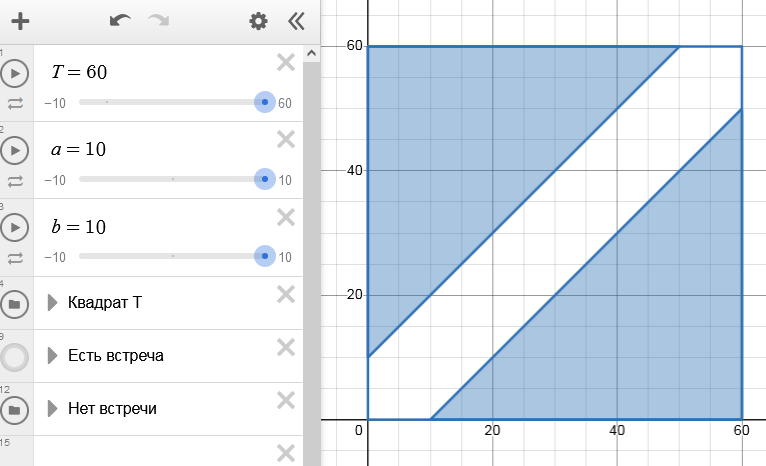
Вероятность равна отношению суммы площадей закрашенных фигур к общей площади квадрата:
$$ P(b)=\frac{1/2\cdot 50^2+1/2\cdot 50^2}{60^2}=0,7 $$Полезная информация
Решебник по вероятности
В решебнике вы найдете более 50 задач о встречах с полными решениями (вводите часть текста для поиска своей задачи):

