Формула Лапласа в Excel
Чуть раньше мы разобрались, как решать задачи на формулу Бернулли, в том числе с помощью удобного шаблона в эксель. Сейчас мы продолжим разбирать задачи на схему независимых повторных испытаний для случая, когда этих испытаний - много, и в ход идут приближенные формулы Лапласа (локальная и интегральная теорема Лапласа) или Пуассона.
Разберем формулы, типовые задачи - решим их вручную и в Excel. Далее вы сможете использовать расчетный файл эксель) для решения своих задач. Удачи!
Локальная и интегральная теоремы Лапласа
В общем виде схема повторных независимых испытаний записывается в виде задачи:
Пусть производится $n$ опытов, вероятность наступления события $A$ в каждом из которых (вероятность успеха) равна $p$, вероятность ненаступления (неуспеха) - соответственно $q=1-p$. Найти вероятность $P_n(k)$, что событие $A$ наступит в точности $k$ раз в $n$ опытах.
Ранее мы привели основную расчетную формулу Бернулли:
$$ P_n(k)=C_n^k \cdot p^k \cdot q^{n-k}=\frac{n!}{k!\cdot(n-k)!} \cdot p^k \cdot q^{n-k}. $$Видно, что в эту формулу входит вычисление факториалов и степеней, и если предположить, что $n$ исчисляется не единицами, а десятками или сотнями, это превращается в сложную вычислительную задачу. Покажем на примере:
Пример 1. Произвели 200 выстрелов. Вероятность попадания при одном выстреле равна 0,6. Найти вероятность того, что при этом будет: 1) ровно 120 попаданий; 2) от 110 до 120 попаданий в цель.
Решение. В этой задаче $n=200$, $p=0,6$, $q=1-p=1-0,4$. Найдем вероятность, что будет ровно $k=120$ попаданий. Подставляем все в формулу выше и получаем:
$$ P_{200}(120)=C_{200}^{120} \cdot 0,6^{120} \cdot 0,4^{80} = \frac{200!}{120!\cdot 80!}\cdot 0,6^{120} \cdot 0,4^{80}=0,05751. $$При этом факториалы вроде $120!$ или степени $0,6^{120}$ "прожует" только математический калькулятор или программа.
Еще страшнее расчеты становятся, когда мы переходим к необходимости вычислить вероятность того, что число попаданий попадет в некоторый промежуток (в нашем случае от 110 до 120) - это уже 11 таких слагаемых, как выше:
$$ P_{200}(110\le k \le 120)= P_{200}(110)+P_{200}(111)+...+P_{200}(120)= \\ = C_{200}^{110} \cdot 0,6^{110} \cdot 0,4^{90} + C_{200}^{111} \cdot 0,6^{111} \cdot 0,4^{89}+...+C_{200}^{120} \cdot 0,6^{120} \cdot 0,4^{80} = 0,46135. $$
И сейчас не у каждого можно найти математический пакет, который рассчитает такую вероятность, а про 18-ый век и говорить нечего. И всех спас Пьер-Симон Лаплас, французский математик. Сегодня эти формулы называют сокращенно формулами Лапласа, Муавра-Лапласа или теоремами Лапласа.
Формулы действуют в предположении, что $n$ – велико, а $р$ – отлично от 0 и 1, так что $npq \ge 9$. При значениях вероятностей близких к 0 или 1 формула дает очень сильную погрешность, в этом случае рекомендуется использовать приближенную формулу Пуассона.
Локальная теорема Лапласа
$$ P_n(k) \approx \frac{1}{\sqrt{npq}}\cdot\varphi \left( \frac{k-np}{\sqrt{npq}}\right), \quad (L1) $$где $\varphi (x)=\frac{1}{2\pi}\cdot exp(-x^2/2)$ - функция Гаусса.
Интегральная теорема Лапласа
$$ P_n(k_1 \le k \le k_2) \approx \Phi \left( \frac{k_2-np}{\sqrt{npq}}\right)-\Phi \left( \frac{k_1-np}{\sqrt{npq}}\right), \quad (L2) $$где $\Phi(x)=\frac{1}{\sqrt{2\pi}}\cdot \int_0^x exp(-t^2/2) dt$ - функция Лапласа (стандартная, или нормированная).
Таблицы значения для функций Гаусса и Лапласа обычно приведены в конце любых учебников по теории вероятностей, в pdf-формате вы можете их скачать на странице формул по ТВ.
При этом иногда функция Лапласа задается выражением $erf(x)=\frac{2}{\sqrt{\pi}}\cdot \int_0^x exp(-t^2) dt $ (функция ошибок, интеграл вероятности), тогда значения в таблице и формулы будут немного иными (сверяйтесь с конкретным учебником или методичкой).
Основные свойства функций, которые пригодятся в решении задач:
$$ \varphi (-x)=\varphi (x), \quad \Phi (-x)=-\Phi (x), \quad \Phi (0)=0; $$ $$ \mbox{при больших x верно:} \quad \varphi (x) \approx 0, \quad \Phi (x) \approx 0,5. $$Вычислим значения вероятностей для задачи выше по формулам Лапласа:
$$ P_{200}(120) \approx \frac{1}{\sqrt{200\cdot 0,6\cdot 0,4}}\cdot\varphi \left( \frac{120-200\cdot 0,6}{\sqrt{200\cdot 0,6\cdot 0,4}}\right)=\\= 0,144 \cdot\varphi (0) = 0,144 \cdot 0,3989 = 0,0576. $$ $$ P_{200}(110 \le k \le 120) \approx \Phi \left( \frac{120-200\cdot 0,6}{\sqrt{200\cdot 0,6\cdot 0,4}}\right)-\Phi \left( \frac{110-200\cdot 0,6}{\sqrt{200\cdot 0,6\cdot 0,4}}\right) =\\= \Phi (0)- \Phi(-1,44)= \Phi (0)+ \Phi(1,44)=0+0,4255=0,4255. $$Видно, что в первом случае значения близки $0,05751 \approx 0,58$, во втором погрешность довольно значительна: $0,46135 \gt 0,4255$.
Формулы Лапласа в Эксель
А теперь рассмотрим, как использовать Excel для вычисления вероятностей в подобных задачах. Для нахождения значений функций вводим следующее: $\Phi(x)$ =НОРМСТРАСП($х$)-0,5, $\varphi (x)$ =НОРМРАСП($х$;0;1;0).
Покажем на примере. На листе подкрашены ячейки (серые), куда можно ввести параметры задачи $n, p, k$ и получить искомые вероятности (текст формулы полностью виден в строке формул вверху).
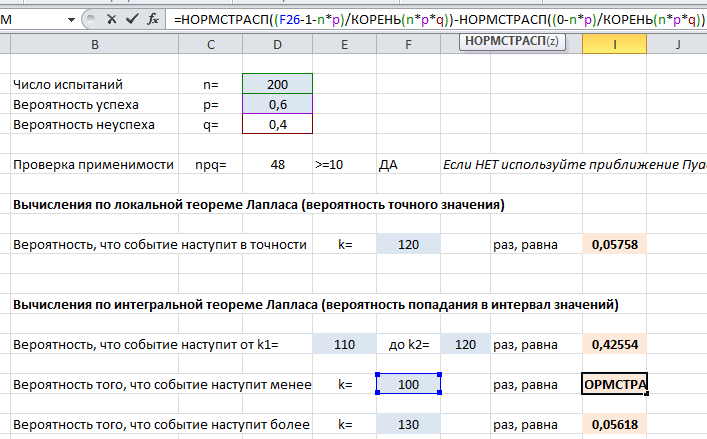
Видно, что расчеты в Эксель для нашей задачи дают те же результаты, что и выше: 0,0576 и 0,4255.
Полезное: расчетный файл c формулами Лапласа
Приближенная формула Пуассона
Рассмотрим сразу случай, когда $n$ большое, а вот вероятность $p$ - очень мала (редкие события), в этом случае требование $npq \ge 10$ не выполняется - формулы Муавра-Лапласа неприменимы, а вычисления по формуле Бернулли весьма трудоемки.
В этом случае обычно используется приближение, названное по имени другого французского математика - формула Пуассона:
$$ P_n(k)= \frac{(np)^k}{k!} \cdot exp (-np) = \frac{\lambda^k}{k!} \cdot exp (-\lambda), \quad \lambda=np \le 10, \quad p \le 0,1. $$Для вычислений в эксель по этой формуле можно вводить либо непосредственно саму формулу, например: =СТЕПЕНЬ(lambda;k)/ФАКТР(k)*EXP(-lambda) или использовать встроенную функцию =ПУАССОН(k;lambda;1) (удобно для вычисления попадания числа наступлений события в интервал):
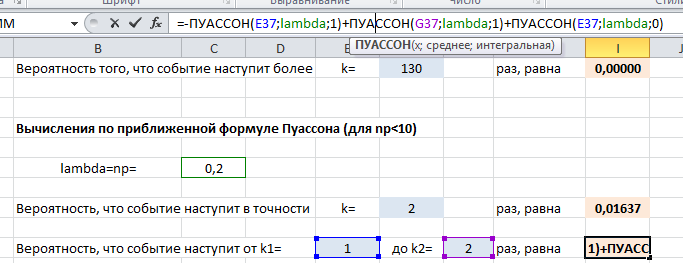
И формулы Лапласа, и Пуассона внесены в один шаблон Excel, будьте внимательны, выбирайте те приближения, которые подходят вашей задаче. Ниже мы разберем несколько примеров со скриншотами.
Также на сайте вы можете найти отдельный онлайн-калькулятор Пуассона
Примеры решений задач
Пример 1. Стрелок выполнил 400 выстрелов, вероятность одного попадания 0,8. Найти вероятность того, что он попал от 310 до 325 раз.
Решение. Получаем, что в задаче идет речь о повторных независимых испытаниях (выстрелах), всего их $n=400$, вероятность попадания при каждом одинакова и равна $p=0,8$, вероятность промаха $q=1-p=1-0,8=0,2$. Нужно найти, что будет от 310 до 325 попаданий. Так как $np=400 \cdot 0,8\cdot 0,2 = 64 \gt 10$, можно использовать для вычисления интегральную теорему Лапласа (L2):
$$ P_{400}(310 \le k \le 325) \approx \Phi \left( \frac{325-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}}\right)-\Phi \left( \frac{310-400\cdot 0,8}{\sqrt{400\cdot 0,8\cdot 0,2}}\right) =\\= \Phi (0,63)- \Phi(-1,25)= \Phi (0,63)+ \Phi(1,25)=0,234+0,3944=0,6284. $$А вот это решение в файле эксель:
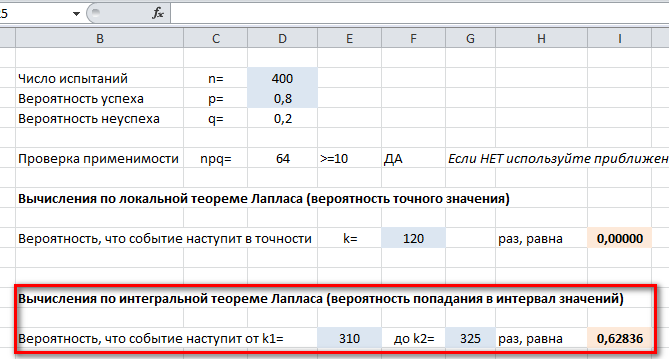
Пример 2. Игральный кубик подбросили 125 раз. Какова вероятность того, что цифра 2 появилась не более 40 раз? Более 30 раз?
Решение. Сначала запишем данные задачи: $n=125$ (число бросков), $p=1/6=0,1667$ (вероятность выпадения цифры 2), $q=1-p=5/6$. Снова обратимся к формулам Лапласа.
Найдем вероятность, что цифра 2 появилась не более 40 раз, то есть от 0 до 40 выпадений случилось:
$$ P_{125}(0 \le k \le 40) \approx \Phi \left( \frac{40-125\cdot 1/6}{\sqrt{125\cdot 1/6\cdot 5/6}}\right)-\Phi \left( \frac{0-125\cdot 1/6}{\sqrt{125\cdot 1/6\cdot 5/6}}\right) =\\= \Phi (4,6)- \Phi(-5)= \Phi (4,6)+ \Phi(5)=0,49999+0,5=0,99999. $$Найдем вероятность, что цифра 2 появилась более 30 раз, то есть от 31 до 125 раз:
$$ P_{125}(31 \le k \le 125) \approx \Phi \left( \frac{125-125\cdot 1/6}{\sqrt{125\cdot 1/6\cdot 5/6}}\right)-\Phi \left( \frac{31-125\cdot 1/6}{\sqrt{125\cdot 1/6\cdot 5/6}}\right) =\\= \Phi (25)- \Phi(2,44)= 0,5-0,4927=0,0073. $$Проведем эти же расчеты в нашем шаблоне эксель, вводя данные задачи в серые ячейки:

Видно, что ответы совпадают.
Пример 3. Аппаратура состоит из 1000 элементов. Вероятность отказа одного элемента за время Т равна 0,001 и не зависит от работы других элементов. Какова вероятность отказа не менее двух элементов.
Решение. Традиционно, начнем с формализации задачи: $n=1000$ (число элементов в аппаратуре), $p=0,001$ (вероятность отказа одного элемента), $q=1-p=0,999$. Видим, что значение $n$ очень велико, а вероятности отказа $p$ редки, так что $npq=0,999 \lt 10$, то есть приближение Лапласа неприменимо, зато отлично подойдет формула Пуассона.
Обозначим $\lambda = np=1000 \cdot 0,001 = 1$, тогда вероятность наступления ровно $k$ отказов элементов можно найти по формуле:
$$ P_n(k)= \frac{\lambda^k}{k!} \cdot e^{-\lambda} = \frac{1^k}{k!} \cdot e^{-1} = \frac{1}{k!} \cdot e^{-1} . $$Найдем вероятность отказа не менее двух элементов:
$$ P_{1000}(k \ge 2)=1-P_{1000}(k \lt 2)=1-P_{1000}(0)-P_{1000}(1)=\\=1-\frac{1}{0!} \cdot e^{-1}-\frac{1}{1!} \cdot e^{-1}=1-2e^{-1} \approx 0,264. $$Найдем эту же вероятность с помощью нашего расчетного шаблона:

Решайте свои задачи и советуйте наш сайт друзьям. Удачи!
Полезные ссылки
Файл эксель для расчетов по формулам Лапласа и Пуассона

