Решение производственной задачи в Excel 2007 и новее
Начало работы
В данном разделе мы рассмотрим, как можно решить производственную задачу в программе Microsoft Excel версий 2007, 2010, 2013 или 2016. Если у вас более старая версия программы Microsoft Excel, то перейдите в другой раздел.
Итак, запустим Microsoft Excel, и перейдем на вкладку "Данные". Справа должна располагаться кнопка "Поиск решения", как на картинке:
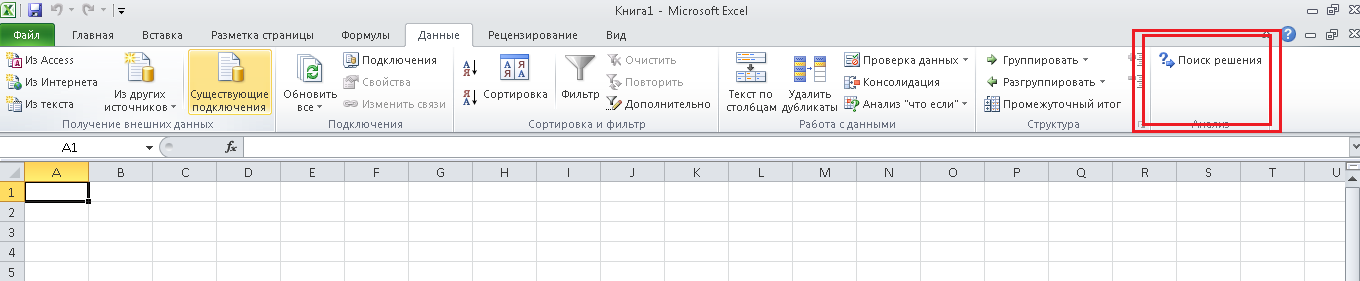
Если же этой кнопки нет, то необходимо включить соответствующую надстройку. Для этого откроем меню файл, и выберем пункт "Параметры":
В открывшемся меню необходимо выбрать пункт "Надстройки":
Затем в правой части, внизу, необходимо выбрать из выпадающего списка "Надстройки Excel", если они еще не выбраны, и нажать кнопку "Перейти":

Появится следующее окно, в котором необходимо отметить галочкой необходимую надстройку (Поиск решения), и нажать кнопку "ОК". После этого на вкладке Данные, в правой части должна появиться показанная выше кнопка
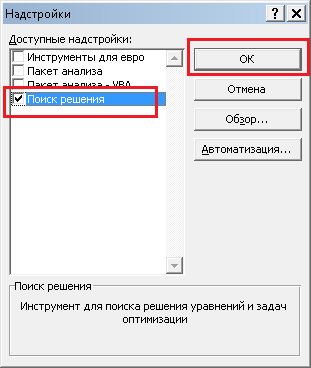
Пример решения ЗЛП в Excel 2010
Возьмем ту же задачу, которую мы решали в предыдущем разделе, и попытаемся решить с помощью компьютера:
| Ресурс | Изделие A | Изделие B | Изделие C | Сколько ресурса на складах |
| R1 | 1 | 2 | 3 | 35 |
| R2 | 2 | 3 | 2 | 45 |
| R3 | 3 | 1 | 1 | 40 |
| Прибыль | 4 | 5 | 6 |
Как мы помним из предыдущего раздела, наши ограничения и целевая функция выглядят следующим образом
$$\begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {{x_A} + 2{x_B} + 3{x_C} \le 35}\\ {2{x_A} + 3{x_B} + 2{x_C} \le 45}\\ {3{x_A} + {x_B} + {x_C} \le 40} \end{array}} \right.\\ {x_A},{x_B},{x_C} \ge 0\\ F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} \to \max \end{array}$$Мы будем заносить данные в следующие ячейки листа Excel:
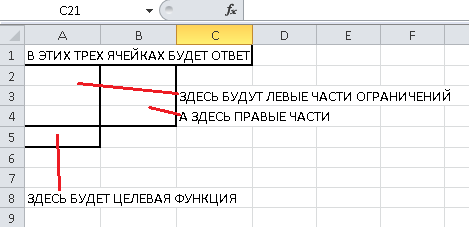
Итак, начнем заполнение. В верхние три ячейки нужно занести ответ, то есть, количество производимых изделий A, B и C. Так как ответ мы не знаем (а иначе зачем бы мы задачу решали), то пока занесем туда три нуля:
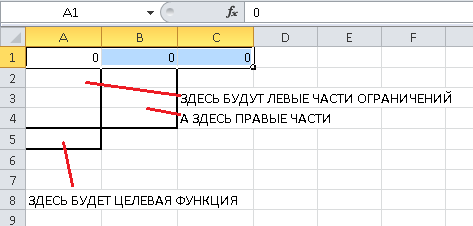
Занесем левые и правые части ограничений в соответствующие ячейки. Например, для первого ограничения ${x_A} + 2{x_B} + 3{x_C} \le 35$ нам нужно занести в ячейку A2 формулу "=A1+2*B1+3*C1", а в ячейку B2 - правую часть ограничения - 35. Точно так же занесем и два других ограничения. Не стоит пугаться, что в ячейках A2-A4 пока будут нули - это естественно, так как пока наше "решение" состоит в том, чтобы не производить ни одного изделия. Должно получиться следующее (красным цветом выделено значение ячейки A4, то есть, третье ограничение $3{x_A} + {x_B} + {x_C} \le 40$):
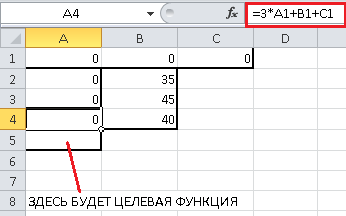
Точно так же, в ячейку A5 занесем формулу для целевой функции $F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C}$ - в Excel это будет формула "=4*A1+5*B1+6*C1". Точно так же, не обращаем внимания, что результатом будет 0 - это естественно, ведь целевая функция представляет из себя прибыль предприятия, а раз мы ничего не производим, то естественно, получаем нулевую прибыль:
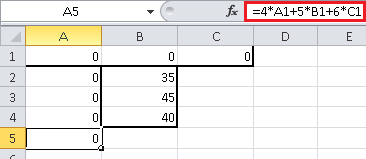
Мы занесли все необходимые данные, теперь необходимо выполнить поиск решения. Для этого на вкладке "Данные" нажимаем кнопку "Поиск решения". Видим следующее окно:
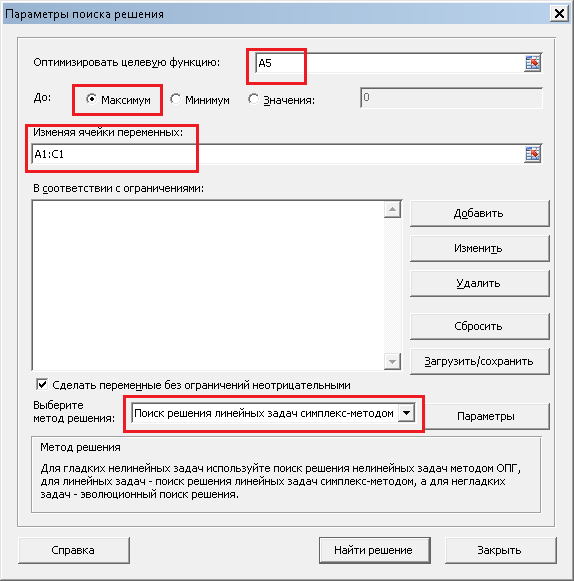
В поле "Оптимизировать целевую функцию" записываем A5, так как именно в ячейке A5 у нас записана целевая функция. На следующей строке выбираем "Максимум", так как нам необходимо максимизировать целевую функцию, то есть, прибыль. В поле "Изменяя ячейки переменных" записываем A1:C1, так как в ячейках A1, B1 и C1 у нас количество производимых товаров, которые необходимо подобрать. В поле "Выберите метод решения" выбираем "Поиск решения линейных задач симплекс-методом". Теперь необходимо задать ограничения. Для этого нажимаем на кнопку "Добавить", и пишем (для первого ограничения) следующее:
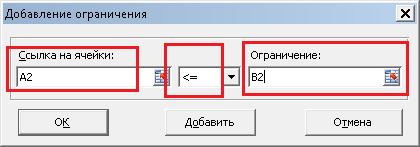
То есть, говорим, что значение ячейки A2 (первое ограничение) должно быть "меньше или равно" значению ячейки B2 (правой части первого ограничения). Нажимаем OK, и ограничение добавится в список. Таким же образом добавляем два других ограничения, а также еще три ограничения - что наши переменные должны быть больше или равны нулю. Должно получиться следующее:
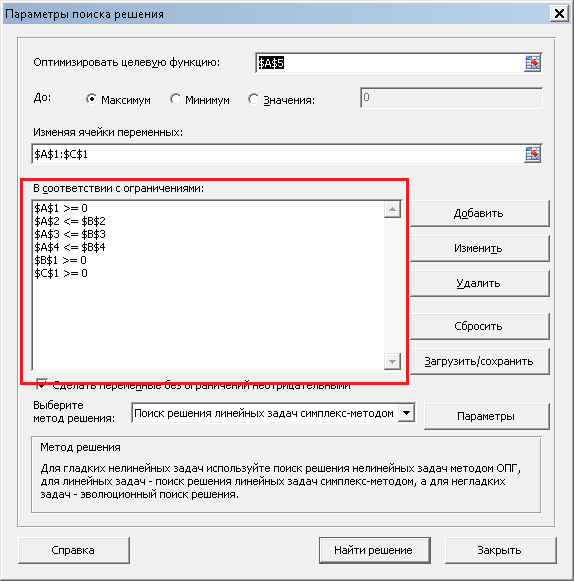
Задача почти решена. Просто нажимаем кнопку "Найти решение", и появляется окно, в котором нам сообщают, что задача решена (решение найдено), а также спрашивают, хотим ли мы его сохранить:
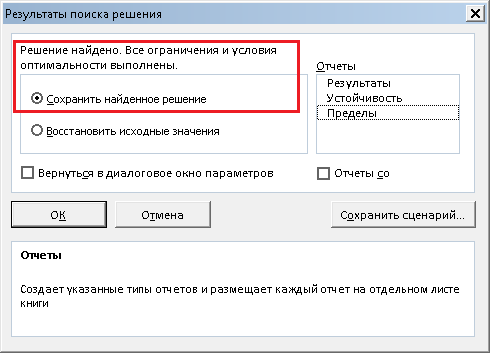
Нажимаем OK, и видим решение в ячейках A1, B1, C1:
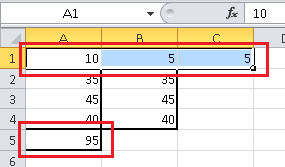
В ячейке A1 мы видим число 10 - число изделий A, которые необходимо произвести, в ячейке A2 - число 5 - число изделий B, которые необходимо произвести, а в ячейке A3 - число 5 - число изделий C, которые необходимо произвести. То есть, мы получили решение (10;5;5) - такое же, как и в предыдущем разделе. Кроме того, в ячейке A5 мы видим максимальное значение целевой функции - тоже, такое же, как и в предыдущем разделе. Задача решена верно.
Конечно, мы решили задачу совсем без оформления. Если вам нужно решить такую задачу для сдачи в университет, то вы можете оформить ее, например, так:
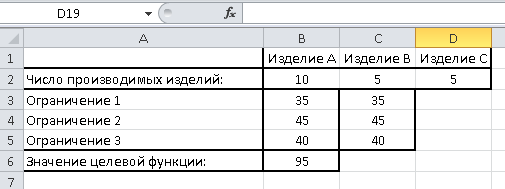
Итоги
Мы научились решать производственную задачу с помощью надстройки Excel под названием "Поиск решения". В следующем разделе мы рассмотрим решение целочисленной производственной задачи, то есть задачи ЛП с дополнительным ограничением - все значения переменных должны быть целыми.
Далее: 2.1.4. Решение ЗЛП в Excel 2003, 2.1.5. Целочисленное решение ЗЛП

