Непрерывная случайная величина

Ранее мы представили примеры решений задач о дискретной случайной величине, теперь переходим к непрерывной. Формально в задачах требуется найти тоже самое: вычислить числовые характеристики, начертить графики, определить неизвестные параметры, найти вероятности событий.

Но формулы-то совсем другие (в силу непрерывности СВ), поэтому стоит разобраться в них хорошенько. Надеемся, наши примеры вам помогут (а если нет времени, закажите решение).

Ниже вы найдете примеры решений на самые разные законы распределений непрерывных случайных величин: законы $\arcsin$ и $\arctan$, тригонометрические и логарифмические функции, показательный, равномерный закон распределения, законы Коши, Симпсона, Лапласа и т.д.

Примеры для других НСВ: Нормальный закон, Равномерный закон, Показательный закон.

Примеры решений

Задача 1. Случайная величина X задана дифференциальной функцией распределения

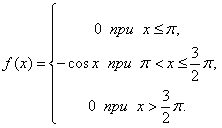
1) Определить вероятность попадания случайной величины X в интервал $[\pi, 5/4 \pi]$.
2) Найти математическое ожидание и дисперсию случайной величины X.

Задача 2. Случайная величина X задана плотностью вероятности:

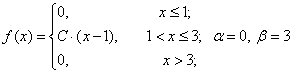
Требуется:
а) найти коэффициент C;
б) найти функцию распределения F(x);
в) найти M(X), D(X), σ(X)
г) найти вероятность P(α < X < β);
д) построить графики f(x) и F(x).

Задача 3. Случайная величина Х задана функцией распределения F(x).
А) является ли случайная величина Х непрерывной?
Б) имеет ли случайная величина Х плотность вероятности f(X)? Если имеет, найти ее.
В) постройте схематично графики f(X) и F(X).

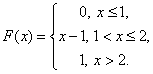
Задача 4. Дана функция распределения F(x) непрерывной случайной величины X.
1. Найти значения параметров a,b
2. Построить график функции распределения F(x)
3. Найти вероятность P(α < X < β)
4. Найти плотность распределения p(x) и построить ее график.

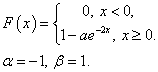
Задача 5. Время в годах безотказной работы прибора подчинено показательному закону, т.е. плотность распределения этой случайной величины такова: f(t)=2e^-2t при t ≥ 0 и f(t)=0 при t<0.
1) Найти формулу функции распределения этой случайной величины.
2) Определить вероятность того, что прибор проработает не более года.
3) Определить вероятность того, что прибор безотказно проработает 3 года.
4) Определить среднее ожидаемое время безотказной работы прибора.

Задача 6. Функция распределения вероятностей случайной величины $X$ имеет вид:

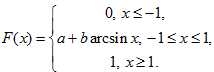
А) найти $a$ и $b$;
Б) найти плотность $f(x)$;
В) нарисовать график $F(x)$;
Г) нарисовать график $f(x)$;
Д) найти $M[X]$;
Е) найти $D[X]$.

Задача 7. Функция распределения вероятностей случайной величины $X$ имеет вид: $$F(x)=A+B \arctan (x/2), -\infty \lt x \lt \infty $$ (закон Коши).
А) определить постоянные $A$ и $B$;
Б) найти плотность распределения вероятностей
В) найти $P(-1 \lt X \lt 1)$;
Г) нарисовать график $F(x)$;
Д) нарисовать график $f(x)$.

Задача 8. Случайная величина $X$ имеет распределение Парето с плотностью вероятности $f(x)=4/23(23/x)^5$ при $23 \le x$ и $f(x)=0$ при $x \lt 23$.
Найдите $M(X)$ и $P(23\lt X \lt 27)$.

Задача 9. Непрерывная случайная величина задана интегральной функцией (функцией распределения) $F(x)$. Найти:
А) вероятность попадания случайной величины $X$ в интервал $(a;b)$.
Б) дифференциальную функцию (функцию плотности вероятностей) $f(x)$.
В) математическое ожидание, дисперсию и среднее квадратическое отклонение величины $X$.
Г) построить графики функций $F(x)$ и $f(x)$.

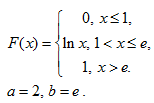
Задача 10. Случайная величина $X$ подчинена закону Лапласа $p(x)=a\cdot e^{-\lambda |x|}$, $\lambda \gt 0.$ Найти $a$, $M(x)$, $D(x)$ и $F(x)$. Построить графики $p(x)$ и $F(x)$.

Задача 11. Случайная величина $X$ задана функцией распределения $F(x)$. Найти:
5) дифференциальную функцию $f(x)$ (плотность распределения),
6) математическое ожидание $M(X)$, дисперсию $D(X)$, среднее квадратическое отклонение $\sigma(X)$.
7) Моду $Mo$ и медиану $Me$,
8) $P(1/2 \lt X \lt 2).$
Построить графики функции и плотности распределения.

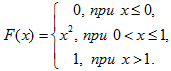
Задача 12. Случайная величина $Х$ подчинена закону Симпсона (закону равнобедренного треугольника) на участке от $-a$ до $+a$.
а) Написать выражение для плотности распределения.
б) Построить график функции распределения.
в) Определить числовые характеристики случайной величины Х.

Решебник по теории вероятности онлайн

Больше 16000 решенных и оформленных задач по теории вероятности: