Цепи Маркова. Переходные вероятности
Примеры решений
Задача 1. Для заданной матрицы переходных вероятностей Р найти вероятности перехода за 2 шага и стационарные вероятности, если они существуют.
Задача 2. Задана матрица $P_1$ вероятностей перехода дискретной цепи Маркова из состояния $i (i=1,2)$ в состояние $j (j=1,2)$ за один шаг. Распределение вероятностей по состояниям в момент $t=0$ определяется вектором $\bar{q}$. Найти:
1) матрицу $P_2$ перехода из состояния $i$ в состояние $j$ за два шага;
2) распределение вероятностей по состояниям в момент $t=2$;
3) вероятность того, что в момент $t=1$ состоянием цепи будет $i=2$;
4) стационарное распределение.
Задача 3. В заданной матрице $L$ элемент $\lambda_{ij}$ есть интенсивность случайного пуассоновского процесса переходов из состояния $i$ в состояние $j$ (размерность кол-во переходов в единицу времени).
А) построить граф переходов между состояниями, ребра которого помечены соответствующими интенсивностями переходов.
Б) написать систему уравнений для определения предельных вероятностей различных состояний.
В) решить эту систему уравнений, найти предельную вероятность каждого состояния.
Задача 4. Найти стационарные вероятности и математическое ожидание для марковского процесса N, заданного графом переходов состояний.
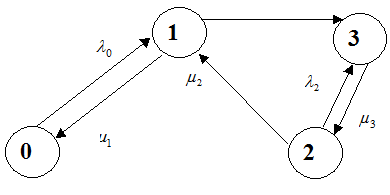
Задача 5. Дан размеченный граф состояний системы.
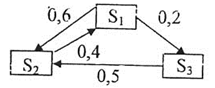
Найти:
А) матрицы перехода за один и два шага,
Б) вероятности состояний системы после первого, второго, третьего шага, если в начальный момент система находилась в состоянии $S_1$,
В) финальные вероятности.
Задача 6. Система имеет три состояния. Построить граф состояний системы, написать уравнения Колмогорова и найти стационарное распределение.

