Примеры решений задач: функция полезности
В этом разделе вы найдете подробно решенные задачи, касающиеся функции полезности, задачи выбора потребителем набора благ при заданном бюджетном ограничении, максимизации полезности, заменяемости товаров и т.д.
Функция полезности: задачи с решениями
Задача 1. Функция полезности имеет вид: $TU=4xy$, где X и Y - количество товаров. Расходы потребителя на эти два товара в месяц равны 1200 р., цена товара X - 400 р., товара Y - 300 р. Определите оптимальный объем ежемесячных закупок двух данных товаров и соответствующее ему значение общей полезности.
Задача 2. Условия: потребитель расходует 200 руб. в неделю на покупку товаров А и В.
Цена (руб.) Кол-во покупаемых единиц товаров Общая полезность Предельная полезность
А 7 20 500 20
В 5 12 1000 30
Задание: Объяснить, как должен поступать потребитель, чтобы максимизировать получаемую полезность при данном бюджете.
Задача 3. Потребитель покупает три товара Х, Y, Z, цены которых соответственно равны Px=100 руб.; Py=70 руб.; Pz=50 руб.
Функции общей полезности разных благ: $F(TU(x))=3\sqrt{Qx}$, $F(TU(y))=5\sqrt{Qy}$, $F(TU(z))=5\sqrt{Qz}$.
Определить:
1) каким образом потребитель может использовать денежный запас 500 рублей для достижения максимальной полезности при потреблении и рассчитать её количественно;
2) то же, если при покупке более, чем 2-х товаров Px снижается на 25%, а Py – на 50%
Задача 4. Допустим, потребитель имеет доход 200 ден. ед. На рисунке показаны две бюджетные линии (I и II) и соответствующие им кривые безразличия.
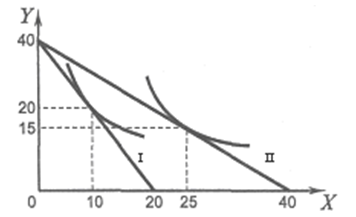
Определить координаты (P,Q) двух точек линии спроса данного потребителя на товар Х.
Задача 5. Общая полезность благ $\alpha$ и $\beta$ для некоего потребителя описывается уравнениями $U_\alpha = q_\alpha(15 - 0,5q_\alpha)$, $U_\beta = q_\beta(30 - q_\beta)$. Допустим, потребитель располагает бюджетом для покупки $\alpha$ и $\beta$ в размере 120 руб., цены на $\alpha$ и $\beta$ равны соответственно 5 и 10 руб. Определить количество $\alpha$ и $\beta$, максимизирующее полезность потребителя.
Задача 6. Потребитель тратит 7 долларов в день на товары X и Y. MU товара X для него равна $10 – x$, где $x$ - количество X в шт. MU товара Y: $21 – 2y$, где $y$ - количество Y в шт. Р 1 ед. товара X = 1 доллар, P 1 ед. Y = 1 доллар. Какое количество X и Y купит рациональный покупатель?
Задача 7. В таблице представлена предельная полезность для походов в магазин.
Имея 100 руб. 80 коп. потребитель купил 3 буханки хлеба по цене 8 руб. за буханку, 4 пакета молока по 11 руб. 20 коп. за пакет и 2 пачки сахара по 16 руб. за пачку. Достиг ли он максимума полезности? Ответ обосновать и в случае отрицательного ответа определить объем покупок, обеспечивающий максимум полезности при данном бюджете.
Задача 8. Построить кривую безразличия для двух абсолютно взаимозаменяемых товаров: пепси-колы и кока-колы, если их цены за литр равны 8 и 10 ден. ед. при бюджете на их потребление, равном 40 ден. ед.
Задача 9. Индивидуум имеет функцию полезности типа Неймана—Моргенштерна, а элементарная функция полезности строго возрастает и зависит только от одного аргумента (денег). Лотерея 6 долларов и 10 долларов с вероятностями 1/3 и 2/3 и лотерея 3 доллара и 9 долларов с вероятностями 2/3 и 1/3 для него эквивалентны. Что можно сказать о склонности данного индивида к риску?
Задача 10. Пусть функция полезности наборов из двух товаров $X=(x_1,x_2)$ имеет вид $u(x_1,x_2)=x_1^{1/7}x_2^{1/6}$.
• Найти набор товаров, который имеет такую же полезность, как набор $X_1=(5,3)$ и количество второго товара равно 1.
• Для набора $X_1=(5,3)$ найти предельные полезности первого и второго товаров.
• В наборе $X_1=(5,3)$ количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
Задача 11. Функция полезности потребителя имеет вид $u(x_1,x_2)=(x_1-50)^{1/7}(x_2-40)^{1/6}$.
1. Найти равновесный спрос и его полезность, если рыночная цена первого товара $p_1=5$, рыночная цена второго товара $p_2=3$ и потребитель выделяет на приобретение товаров сумму $M=5000$ денежных единиц.
2. Найти функции спроса на оба вида товаров.
3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.
Задача 12. Для потребителя с функцией полезности $U(x_1,x_2)=x_1^{1/3}x_2^{1/4}$
1) найдите функцию спроса на каждый товар;
2) найдите точку спроса при доходе $K=60$ и ценах $P=(2,4)$.
Задача 13. Решить прямую задачу потребителя (найти оптимальную потребительскую корзину). Дано: Функция полезности потребителя $U=\sqrt{xy}$. Цена блага х равна 15, цена блага у равна 20, доход потребителя равен 300.
Найти: Оптимальный набор благ потребителя $(х, у)$.
Задача 14. Предельная полезность первой единицы блага равна 300. При потреблении первых трех единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза. Предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 5 раз. Найти совокупную полезность 5 единиц блага.

